팜테크(FAMTECH)
SDOF 라플라스 변환 분석 (S Plane, Poles, Laplace, Critical Damping, Modal Residue) 본문
SDOF 라플라스 변환 분석 (S Plane, Poles, Laplace, Critical Damping, Modal Residue)
FAMTECH 2023. 8. 16. 10:51
목차
"관련제품 문의는 로고 클릭 또는 공지사항의 연락처를 통해 하실 수 있습니다."
SDOF 라플라스 변환(Laplace Transform)

위 그림과 같이 Spring, Mass, Damper로 구성된 SDOF(Single Degree of Freedom)에 대해 알아보겠습니다.
분석 전에 참고로 아래 모달 분석 장비에 대해 간단하게 소개 드리겠습니다.

위 그림은 SDOF를 Damper가 포함된 모델과 포함되지 않은 모델을 시뮬레이션으로 분석해주고 있습니다. 해당 제품은 팜테크에서 판매 중인 Vibrant 사의 Mescope라는 소프트웨어 입니다. 실제 계측 정보를 통해 분석도 가능 하고 FEA를 통한 시뮬레이션도 가능 합니다. 해당 제품에 관심이 있으시다면 아래 회사 이미지를 클릭해서 홈페이지를 통해 문의 주시면 됩니다. 관련 교육도 제공 하고 있으니 언제든지 방문 문의 주세요~!
다시 SDOF의 라플라스 분석에 대해 알아보겠습니다.
SDOF(LTI) 시스템(단일 자유도 선형 시스템)의 라플라스 변환은 시간 영역에서 동작하는 시스템의 동적 응답을 라플라스 변환을 통해 복소 주파수 영역으로 옮겨 분석하는 과정을 나타냅니다. 이를 통해 복잡한 시간 도메인의 계산을 단순한 대수식 계산으로 전환하여 시스템의 동작을 이해하고 분석하는데 도움이 됩니다.
라플라스 변환은 시간 영역에서의 함수를 복소 평면상의 함수로 변환하는 수학적 기법입니다. SDOF 시스템에서는 시간 도메인의 입력과 출력을 라플라스 변환하여 복소 주파수 도메인으로 옮긴 후, 전달 함수(transfer function)를 사용하여 시스템의 응답을 분석합니다. 전달 함수는 입력과 출력 간의 관계를 표현하는 함수로, 시스템의 라플라스 변환된 입력과 출력을 나눈 것으로 정의됩니다.
라플라스 변환을 사용하면 시스템의 응답을 시간적인 지연이나 지수적 감쇠 등의 수학적 함수로 묘사할 수 있습니다. 이를 통해 시스템의 안정성, 공진 주파수, 감쇠 비율 등을 분석할 수 있습니다.
간단히 말해, SDOF 시스템의 라플라스 변환은 시간 도메인에서 주파수 도메인으로의 변환을 통해 시스템의 동작을 수학적으로 분석하고 예측하는데 사용되는 중요한 도구입니다.

SDOF를 라플라스 변환을 하면 위와 같은 수식으로 전개 됩니다. 이를 입력과 출력의 전달 함수의 형태로 표현하면 아래와 같습니다.

수식2의 s 값을 real과 imaginary 값을 사용해서 그래프로 표현해주면 아래와 같습니다.
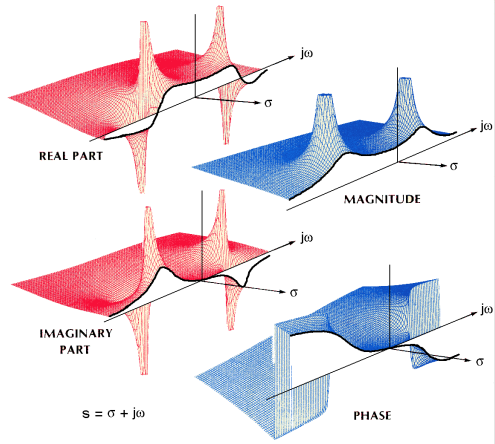
Real Value가 양수(Postive)인 경우는 시스템이 불안전(Unstable)하기 때문에 실제 분석에서는 사용하지 않고 음수 영역에서만 사용 합니다. 그림과 같이 real value가 음수이면서 Magnitude가 끝없이 증폭되는 2개의 포인트를 Pole이라고 부릅니다. 이때는 시스템이 폭주하는 영역이므로 해당 영역을 피한 설계를 하여야 합니다.
SDOF 라플라스 변환과 S-Plane, Pole, Critical Damping, Modal Residue
S-plane은 간단하게 설명하면 그림1을 위에서 본 화면이라고 생각하시면 됩니다.
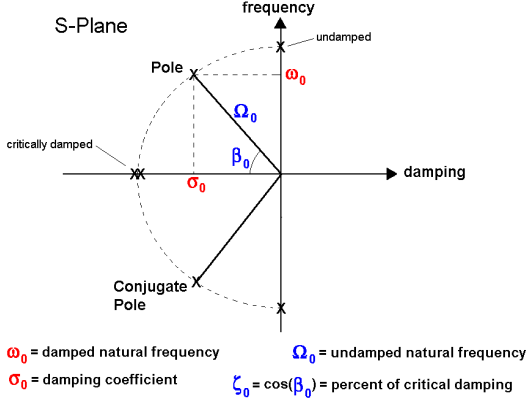
<폴 값(Pole)>
제어 시스템, 신호 처리, 신호 분석 등 다양한 공학 분야에서 "pole"은 시스템의 동작을 나타내는 중요한 개념 중 하나입니다. Pole은 시스템의 라플라스 변환된 전달 함수(transfer function)의 분모 다항식에서의 해(Solution, Root)를 의미합니다.
더 간단하게 말하면, 시스템의 pole은 시스템의 동작을 결정하는 주요 특성이라고 볼 수 있습니다. Pole의 위치는 시스템의 안정성, 응답의 형태, 공진 주파수 등과 관련이 있습니다. Pole이 복소수 평면에서 어떤 위치에 있는지에 따라 시스템의 동작이 달라집니다.
SDOF에서 Pole이란 그림과 같이 전달함수 값이 무한대의 값을 가지게 됩니다.
<Critical damping(임계감쇠)>
Critical damping(임계감쇠)은 진동 시스템에서 감쇠(damping)의 정도를 나타내는 개념 중 하나입니다. 감쇠는 시스템의 진동이 시간이 지남에 따라 감소하는 정도를 나타내며, 시스템이 감쇠되지 않으면 오랜 시간 동안 계속 진동하거나 불안정한 동작을 할 수 있습니다.
임계감쇠란 시스템이 특정한 상태로 수렴하는 데 필요한 최소한의 감쇠 정도를 의미합니다. 이 상태에서는 시스템이 가능한 빠르게 진동을 억제하면서도 진동이 자연적으로 감쇠되어 안정된 상태로 수렴하게 됩니다. 임계감쇠 상태에서는 시스템이 불안정하지 않고, 가능한 빠른 시간 내에 초기 진동이 소멸됩니다.
임계감쇠의 개념은 감쇠비(damping ratio)와 밀접한 관련이 있습니다. 감쇠비는 시스템의 감쇠 정도를 비율로 표현한 값으로, 감쇠비가 1일 때 임계감쇠 상태에 해당합니다. 감쇠비가 1보다 작으면 미약하게 감쇠되는 미감쇠 상태이며, 감쇠비가 1보다 크면 과감쇠 상태로 진동이 너무 빨리 감쇠되는 상태를 나타냅니다.
임계감쇠는 각종 공학 분야에서 중요한 개념으로 사용되며, 특히 구조물의 안정성, 진동 감쇠 시스템의 설계, 제어 시스템 설계 등에서 고려되는 중요한 요소입니다.
<Modal Residue>
"Modal residue"는 주로 공학 및 물리학 분야에서 사용되는 용어로, 특히 선형 시스템의 모드(mode)들의 불안정성을 분석할 때 사용됩니다. 이 용어는 모드 해석(modal analysis)과 관련이 있습니다.
모드 해석은 복잡한 동적 시스템이나 구조물을 여러 개의 기본적인 진동 모드로 분해하여 이해하는 기술입니다. 간단히 말해, 어떤 시스템의 모드는 시스템이 특정 주파수와 진동패턴에서 진동할 때의 형태를 나타냅니다. 모드 해석을 통해 시스템의 동작을 간단한 모드로 분해하여 더 쉽게 이해하고 분석할 수 있습니다.
모드 해석에서 모드의 불안정성을 분석할 때 "modal residue"가 사용될 수 있습니다. Modal residue는 특정 모드의 감쇠된 진폭이나 불안정성을 나타내는 값을 나타냅니다. 불안정한 모드의 경우, 해당 모드의 modal residue는 복소수 평면에서 오른쪽 반평면에 위치할 수 있습니다. 이것은 해당 모드가 시간이 지남에 따라 지수적으로 증가하는 진동을 나타낸다는 것을 의미합니다.
공학 및 물리학 분야에서 모드 해석과 모드의 불안정성 분석은 시스템 설계, 구조물 안정성 평가, 진동 감쇠 제어 등 다양한 응용 분야에서 중요합니다. Modal residue는 시스템의 모드들의 불안정성을 평가하고 이해하는 데 도움을 주는 도구 중 하나입니다.
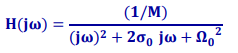
위 수식은 real value가 0일때의 전달함수(Transfer Function) 값입니다.

해당 값은 위와 같이 부분 해로 구할 수 있고 각 Pole 지점에서 real value가 0일때 최대 증폭을 결정하는 값을 알수 있게 됩니다. 해당 파라미터를 Modal Residue라고 합니다.







