[랜덤 진동 시험] Leakage와 Windowing Function(누유 현상과 윈도우 처리, Random Vibration Test)

 

목차

 

 

"관련제품 문의는 로고 클릭 또는 공지사항의 연락처를 통해 하실 수 있습니다."

 

 

 

Discontinuity and Leakage

 

 

푸리에 급수(Fourier series)는 신호가 시간에서 주기적이라는 가정을 합니다. 하지만 대부분의 진동 신호는 시간적으로 주기성을 가지지 않습니다. 따라서 디지털로 변환된 신호에서는 신호의 마지막 샘플과 가정된 주기적 반복의 처음 샘플 사이에 불연속성(Discontinuity)이 발생합니다.

 

이 불연속성은 FFT(Fast Fourier Transform, 고속 푸리에 변환) 알고리즘이 잡음 또는 노이즈를 생성하는 원인이 됩니다. FFT를 적용할 때 신호의 경계에서의 이 불연속성은 스펙트럼 누출(spectral leakage)을 일으키고, 원래 신호에 없는 추가적인 주파수 성분을 생성합니다.

 

이러한 불연속성에 의한 인공적인 잡음을 완화하기 위해 다양한 기법들이 사용됩니다. 일반적인 방법으로는 FFT를 수행하기 전에 신호에 윈도잉(windowing) 함수를 적용하는 것입니다. 윈도잉 함수는 신호의 경계에서 점점 작아지는 가중치를 적용하여 불연속성의 영향을 줄이고 스펙트럼 누출을 최소화합니다. 적절한 윈도잉 함수를 선택함으로써 엔지니어들은 원래 신호의 더 정확한 주파수 표현을 얻고 FFT 알고리즘에 의해 도입된 인공적인 잡음을 줄일 수 있습니다.

 

 

 

The effect of periodic and non-periodic signals (in Time T) on the FFT computation. SR = 2000 samples/sec., N = 1024, Periodic: 23.4375 Hz, Non-periodic: 23.9258 Hz.

 

 

 

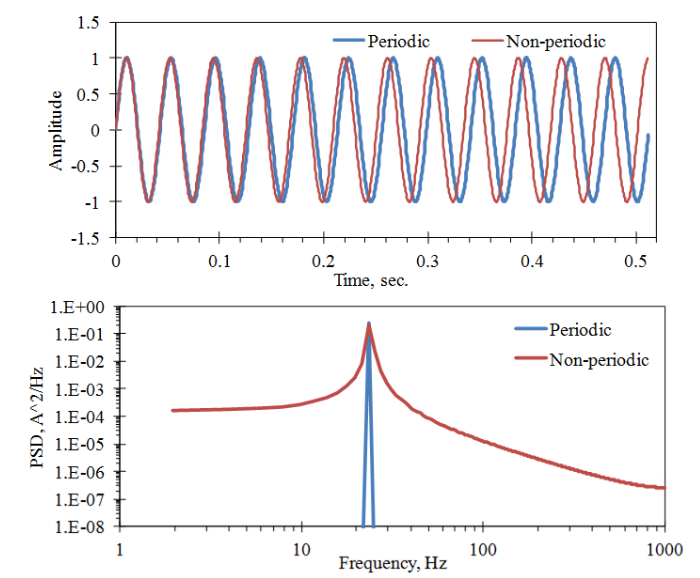
그림은 두 개의 사인파를 사용하여 이 불연속성과 FFT에서 발생하는 잡음을 설명하는 간단한 예시를 보여줍니다. 첫 번째 사인파는 정확하게 샘플된 시간 T = 0.512초에 정수 주기로 맞게 들어갑니다 (시간적으로 주기적인 형태). 두 번째 사인파는 약간의 차이가 있어 (시간적으로 주기적이지 않은 형태) 시간상의 불연속성과 FFT에서 잡음을 생성합니다.

 

사인파의 이론적인 전력 스펙트럼 밀도 (PSD, Power Spectral Density)는 해당 주파수에서의 에너지입니다. 시간적으로 주기적이지 않은 신호로 인한 불연속성은 인접한 주파수에서 퍼지는 가짜 진폭을 생성합니다. 이를 leakage라고 부릅니다.

 

주기적인 사인파의 경우 FFT는 정확하게 주파수 내용을 나타내며, 전력 스펙트럼 밀도는 해당 사인파의 주파수에서의 날카로운 Peak를 보여줍니다. 그러나 시간적으로 주기적이지 않은 사인파의 경우, 시간상의 불연속성으로 인해 주파수 영역에서 왜곡이 발생합니다.

 

시간적으로 주기적이지 않은 사인파의 FFT는 실제 주파수에 인접한 주파수에서 가짜 진폭이나 에너지를 생성합니다. 이 추가적인 진폭은 leakage로 알려져 있으며, FFT 결과에서 잡음(Noise)으로 나타납니다. 시간적으로 주기적이지 않은 사인파의 이론적인 전력 스펙트럼 밀도는 실제 주파수에서만 에너지를 가져야 하지만, 불연속성(Discontinuity)으로 인해 에너지가 인접한 주파수로 퍼지게 됩니다.

 

요약하자면, 신호의 시간적인 주기성 부재는 시간상의 불연속성을 초래하여 FFT에서 스펙트럼 leakage가 발생합니다. 이 leakage는 인접한 주파수에서 가짜 진폭을 만들어내며, 주파수 영역 분석에서 관측되는 잡음의 원인이 됩니다.

 

 

 

 

 

 

 

Windowing Function

 

Hanning window used for a digital sample with SR = 2000 samples/sec. and N = 1024

 

 

스펙트럼 leakage를 줄이기 위해 엔지니어들은 FFT를 계산하기 전에 디지털화된 신호를 수정하는 작업을 수행하는데, 이를 윈도우 함수(windowing)이라고 합니다. 윈도잉은 시간 샘플의 시작과 끝에서 신호를 점점 0으로 수렴하도록 조절하는 것을 의미합니다.

 

 

 

가장 흔히 사용되는 윈도우 함수 중 하나는 Hanning window 입니다. 이 윈도우는 "raised cosine" 윈도우라고도 불리며, 다음과 같은 수식으로 표현됩니다:

 

 

여기서 n은 샘플의 인덱스를 나타내고, N은 신호의 전체 샘플 수를 나타냅니다.

 

Hanning 윈도우는 신호를 중앙에서부터 가장자리로 부드럽게 감소시켜 점점 0으로 수렴하도록 만듭니다. 이 감쇠는 신호 경계에서의 불연속성을 완화하고 FFT 분석에서의 스펙트럼 leakage를 줄이는 데 도움이 됩니다.

 

FFT 계산 이전에 디지털화된 신호에 윈도잉을 적용함으로써 엔지니어들은 leakage의 영향을 줄이고, 주파수 영역에서 원래 신호의 보다 정확한 주파수 표현을 얻을 수 있습니다.

 

Effects of the Hanning window on the examples

 

 

하지만 윈도잉에는 Trade Off가 있습니다.

 

첫째로, 주기적인 신호의 경우에도 Peak 주파수에 인접한 주파수 대역의 전력 스펙트럼 밀도 (PSD) 레벨이 증가합니다. 이를 사이드밴드 leakage라고 합니다. Side Band leakage는 피크 주파수의 정확한 위치를 불확실하게 만들 수 있습니다. 이에 대해서는 다음 레슨인 주파수 해상도에서 더 자세히 다룰 예정입니다.

 

둘째로, 윈도잉은 시간 샘플 내의 신호의 평균 제곱 진폭을 감소시킵니다. 따라서 피크 주파수에서의 PSD 레벨이 감소합니다. 

 

 

 

 

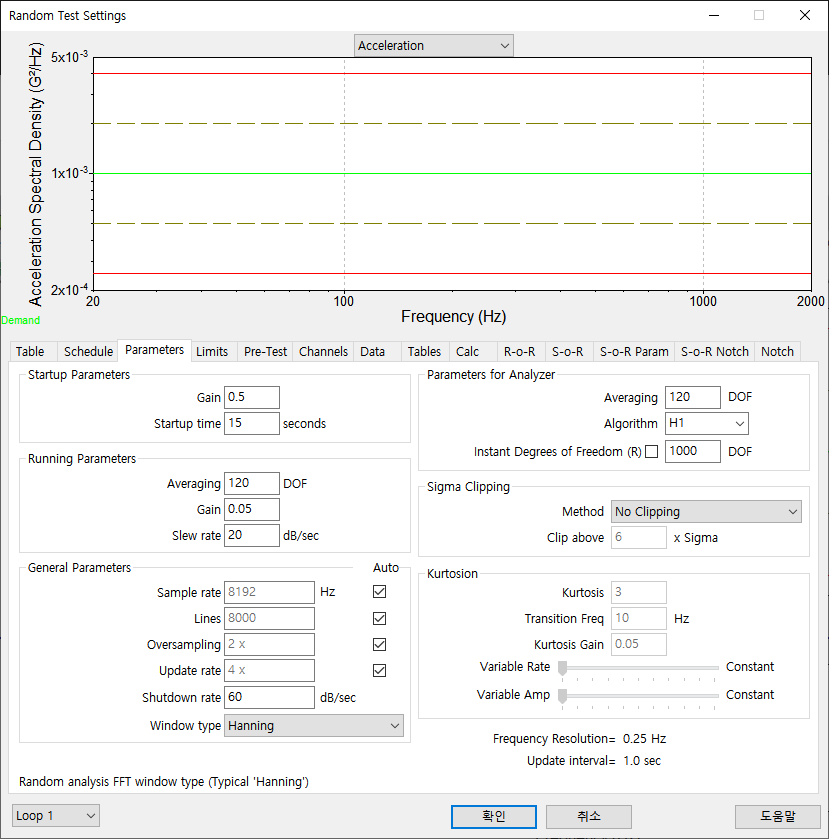
위 그림은 팜테크(FAMTECH)에서 판매 중인 Vibration Research 사의 VibrationVIEW 진동 시험 제어기의 설정 화면 입니다. 기본적으로 Hanning 윈도우가 설정되어 있습니다. 분석하고자 하는 결과 파형에 맞춰 Windwo 함수를 변경해서 사용할 수 있습니다.

 

신호와 윈도우의 관계에 대한 상세 설명은 팜테크 오프라인 교육을 통해 확인하실 수 있습니다.