팜테크(FAMTECH)
푸리에 변환이란, 수식, 특징 정리 (Fourier transform) 본문
목차
푸리에 변환이란? (Fourier transform)
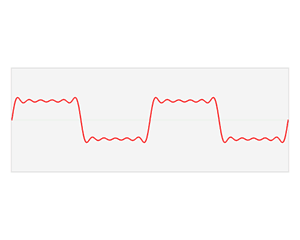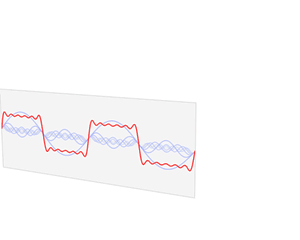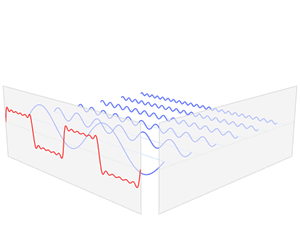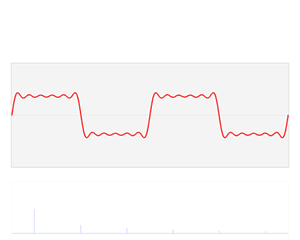
푸리에 변환이란 시간(time)에 따라 변하는 waveform을 주파수(frequency)에 따라 분해 해주는 수학적 함수(function) 입니다. 푸리에 변환이 된 시간 파형은 복소수(complex value)의 주파수 함수가 됩니다.
복소수 주파수 함수에서 절대값(Absolute value)는 원 신호의 진폭(amplitude)이고 complex 값은 위상(phase) 정보입니다.
푸리에 변환은 푸리에 시리즈(Fourier series)의 일반화라고도합니다. 푸리에 시리즈는 주기(periodic)를 가지는 파형을 사인 파형으로 분해해줍니다. 푸리에 변환은 푸리에 시리즈를 비주기(non periodic) 파형까지 확장하는 개념입니다.

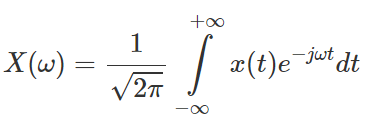

첫 번째 수식은 푸리에 급수(Fourier series)이고 두 번째와 세 번째 수식은 라디안(Radian)과 Hz의 주파수에 따른 수식 입니다.
위 수식에 따라 푸리에 변환을 하기 위해서는 시간함수 파형이 수렴을 해야 합니다. 끊임 없이 증가하는 지수형태의 파형은 푸리에 변환이 안됩니다.
푸리에 변환의 특징
1. 푸리에 변환은 선형(Linear) 입니다.
a(t), b(t) 라는 시간의 함수가 있을 때 푸리에 변환 후 A(f) + B(f) 의 합은 변환 전 a(t)+b(t)에 푸리에 변환 한 것과 같습니다.
2. 시간에 불변합니다.
a(t)의 푸리에 변환과 a(t-x)의 푸리에 변환은 동일 합니다. (x는 실수)
3. Parserval의 이론 : a(t)와 A(f) 사이 1대 1 변환만 됩니다.
4. Time scaling
a(x * t) 와 같이 시간에 어떤 수로 scaling 하면 푸리에 변환의 주파수 bandwidth는 역수로 변화 합니다.
'기초이론' 카테고리의 다른 글
| [Frequency]Decade, Octave 란? 계산 방법 (0) | 2022.02.24 |
|---|---|
| NVH(Noise, Vibration, Harshness)란? (0) | 2021.12.10 |
| 주파수 디지털 필터란? (Frequency Digital Filter, Pass filter, Roll-off) (0) | 2021.12.08 |
| 진동 전달률(Vibration Transmissibility) 이란? (0) | 2021.12.01 |
| FFT 와 DFT 관계 (Fast Fourier Transform vs Discrete Fourier Transform) (0) | 2021.11.19 |





