[ObserVIEW] 복소수 응답 분석: Bode Plot, Nyquist, Complex Response(Bode plot, magnitude response, phase response, gain margin, phase margin, frequency response, 진동 분석, 진동 시험 분석)

 

목차

 

"관련제품 문의는 로고 클릭 또는 공지사항의 연락처를 통해 하실 수 있습니다."

 

 

 

 

복소 응답 분석과 그래프 방식의 배경

 

진동 시험이나 구조 응답 분석에서, 흔히 우리가 다루는 것은 단순한 “진폭 vs 시간”이 아니라, 입력 대비 출력의 진폭 변화뿐 아니라 위상(phase) 변화도 포함하는 복소 응답(complex response) 입니다. 즉, 시스템의 전달함수(transfer function)나 주파수 응답 함수(frequency response function, FRF)는 단순한 실수값이 아니라, 진폭과 위상을 동시에 지닌 복소수(complex number) 로 표현됩니다.

 

이처럼 복소 응답 데이터를 해석할 때, 단순한 시간 영역(time-domain) 그래프만으로는 얻기 어려운 정보 — 예: 어떤 주파수에서 얼마나 증폭되는지, 위상이 얼마나 지연되거나 앞서는지, 모드(mode) 간 결합이나 안정성 여부 등 — 를 파악하기 위해 여러 형태의 시각화 방식이 활용됩니다. 그 중 대표적인 것이 Bode, Complex, Nyquist 그래프입니다.

 

ObserVIEW - 복소 응답 분석, Bode, Complex, Nyquist, 팜테크

 

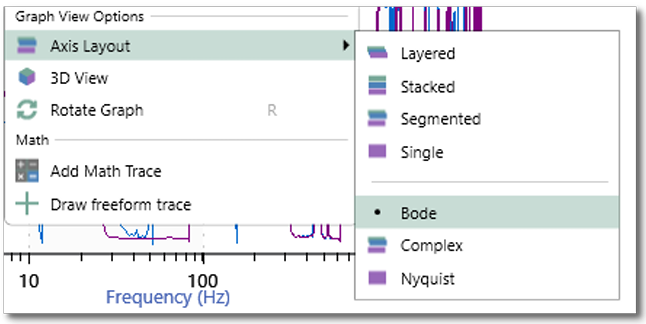
각 그래프는 같은 복소 응답 데이터를 “다르게 투영(projection)”한 결과이며, 보는 각도(주파수 중심인지, 복소 평면(실수/허수) 중심인지 등)에 따라 얻을 수 있는 통찰이 달라집니다. 따라서 상황에 따라 가장 적합한 그래프를 선택하는 것이 중요합니다.

 

 

 

 

Bode Plot — 주파수 응답 특성(증폭/감쇠 & 위상)을 한눈에 보고 싶을 때

 

 

ObserVIEW, 빔 캔틸러버, 진동 시험, Bode Plot 분석, 팜테크

 

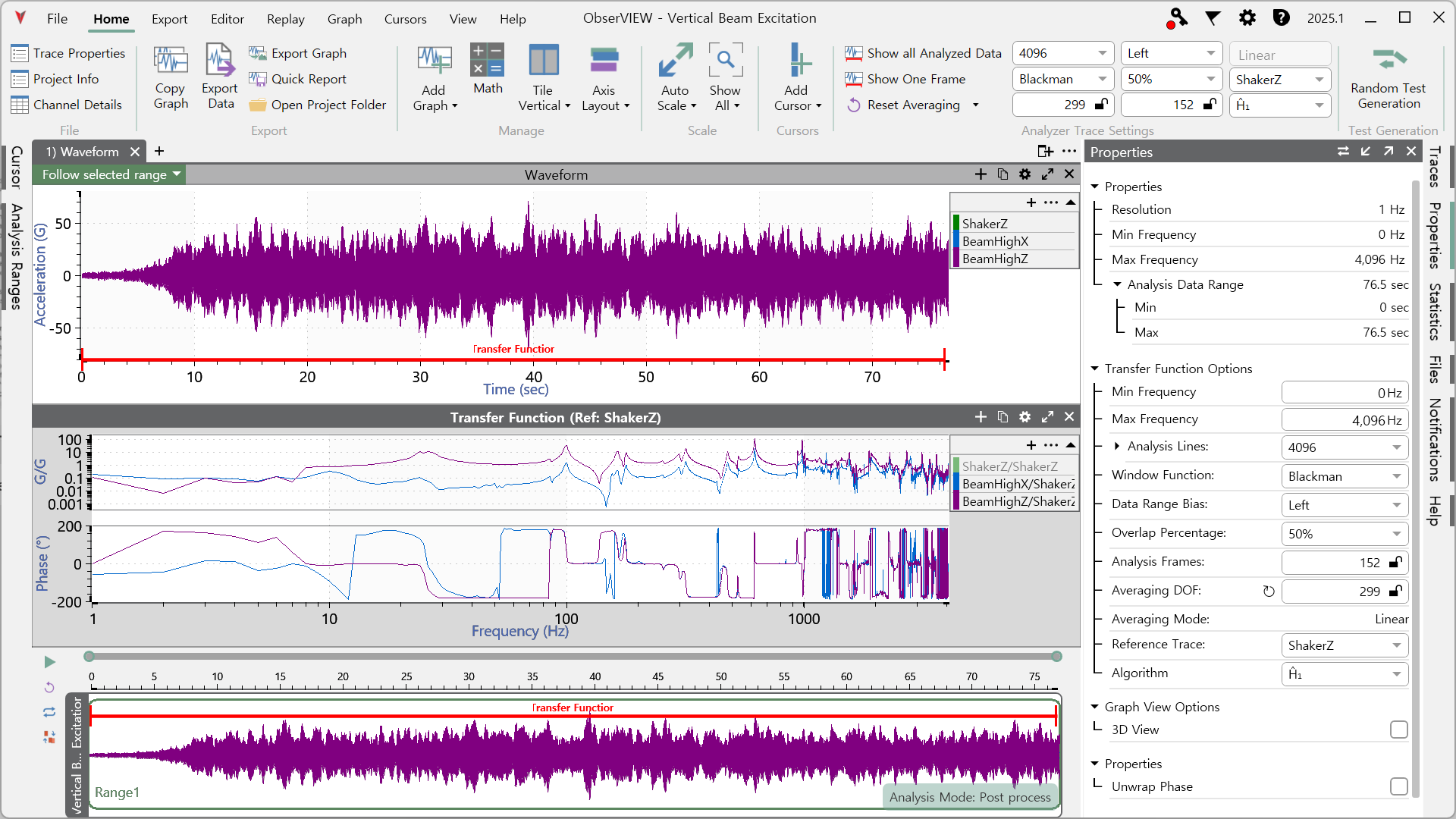
Bode 플롯은 가장 널리 사용되는 방식 중 하나입니다. 이 그래프는 복소 응답을 두 개의 세미로그 플롯으로 나눠 보여줍니다: 하나는 주파수 대비 진폭(또는 이득, gain), 다른 하나는 주파수 대비 위상(phase) 변화입니다. 

 

• 주파수별 증폭 또는 감쇠 특성을 명확히 파악할 수 있습니다. 예를 들어, 어떤 구조물이 특정 주파수에서 공진하여 진폭이 급격히 커지는지, 또는 필터처럼 특정 대역 이하/이상의 주파수를 얼마나 감쇄하는지 쉽게 확인할 수 있습니다.
• 위상 변화도 함께 볼 수 있어, 입력 대비 출력이 시간적으로 얼마나 지연되거나 앞서는지 알 수 있습니다. 이는 특히 제어 시스템이나 감쇠 설계, 구조물의 응답 Time-shift 분석 등에 유용합니다.
• 제어공학 및 시스템 설계 관점에서는 이득 여유(gain margin) 와 위상 여유(phase margin) 같은 안정성 지표를 얻기 쉽습니다. 
• 필터 설계, 구조물/기계의 주파수 응답 특성 확인, 전반적인 주파수 특성 요약 등 “전체 응답 경향을 큰 그림으로 파악”할 때 가장 직관적입니다.

 

따라서, 만약 여러분이 “이 구조, 이 시스템이 특정 주파수에서 어떻게 반응하는가”, 혹은 “어떤 대역이 약하거나 강한가” 같은 주파수 기반 응답 특성을 보고 싶다면, Bode 플롯이 시작점으로 적합합니다. 예를 들어 빔이 1차 굽힘 모드에 진입할 때 위상은 0° 근처에서 시작하여 –90° 부근으로 변하고, 공진을 지나면 –180°에 가까워지는 패턴을 보입니다

 

 

 

 

Complex Plot — 복소 평면 위에서 모드나 공진, 복잡한 응답 거동을 보고 싶을 때

 

ObserVIEW, 빔 캔틸러버, 진동 시험, Complex Plot 분석, 팜테크

 

Complex 플롯은 Bode처럼 주파수 축을 직접 사용하지 않고, 대신 실수부(real) 와 허수부(imaginary) 를 x-축과 y-축으로 하는 복소 평면(complex plane) 위에 응답을 나타냅니다. 즉, 각 주파수에 대응하는 복소 응답 벡터가 복소 평면에서 어떻게 위치하고 움직이는지를 보여줍니다. 이 방식은 주파수를 직접 보는 대신, 응답의 위상과 크기가 복소 평면 상의 점이나 궤적으로 표현됩니다.

이 방식이 유리한 이유는 다음과 같습니다.

(1) 모드(공진)의 존재 여부와 정확한 주파수

Complex Plot에서 Real 또는 Imag 값이 크게 튀거나, 복소평면에서 점들이 갑자기 변하는 지점은 명확한 공진 주파수입니다.
Bode Plot에서도 공진을 볼 수 있지만, Complex Plot에서는 더 선명하게, 부가 신호 없이 공진만을 정확히 확인할 수 있는 장점이 있습니다.

 

(2) 각 모드의 감쇠 특성(damping)

감쇠가 작은 모드는

• Real/Imag의 변화가 매우 가파르며
• 복소평면에서 루프가 길고 얇은 형태로 나타나는 경향이 있습니다.

감쇠가 크면 변화량이 작고 완만하게 나타납니다.

위 그래프는 대부분의 스파이크가 매우 날카롭게 형성되어 있어, 빔의 감쇠가 매우 작고 고품질의 탄성 구조임을 보여줍니다.

 

(3) 구조 모드의 형태(mode shape) 관련 정보

센서 위치가 서로 다르면 동일한 모드에서도

• Real/Imag의 크기
• 스파이크의 방향
• 응답의 부호(positive/negative)

가 달라질 수 있습니다. 이는 기본적으로 모드 형상(mode shape) 에 따라 어떤 위치가 배음(antinode)이고 어떤 위치가 절점(node)에 가까운지를 반영합니다. 그래프에서 각 채널의 패턴이 거의 동일함은 해당 위치들이 같은 모드 형상에서 유사한 운동 방향을 가진 위치임을 의미합니다.

 

 

 

 

Nyquist Plot — 복소 평면 + 제어/안정성 혹은 모달 안정성까지 함께 보고 싶을 때

 

ObserVIEW, 빔 캔틸러버, 진동 시험, Nyquist Plot 분석, 팜테크

 

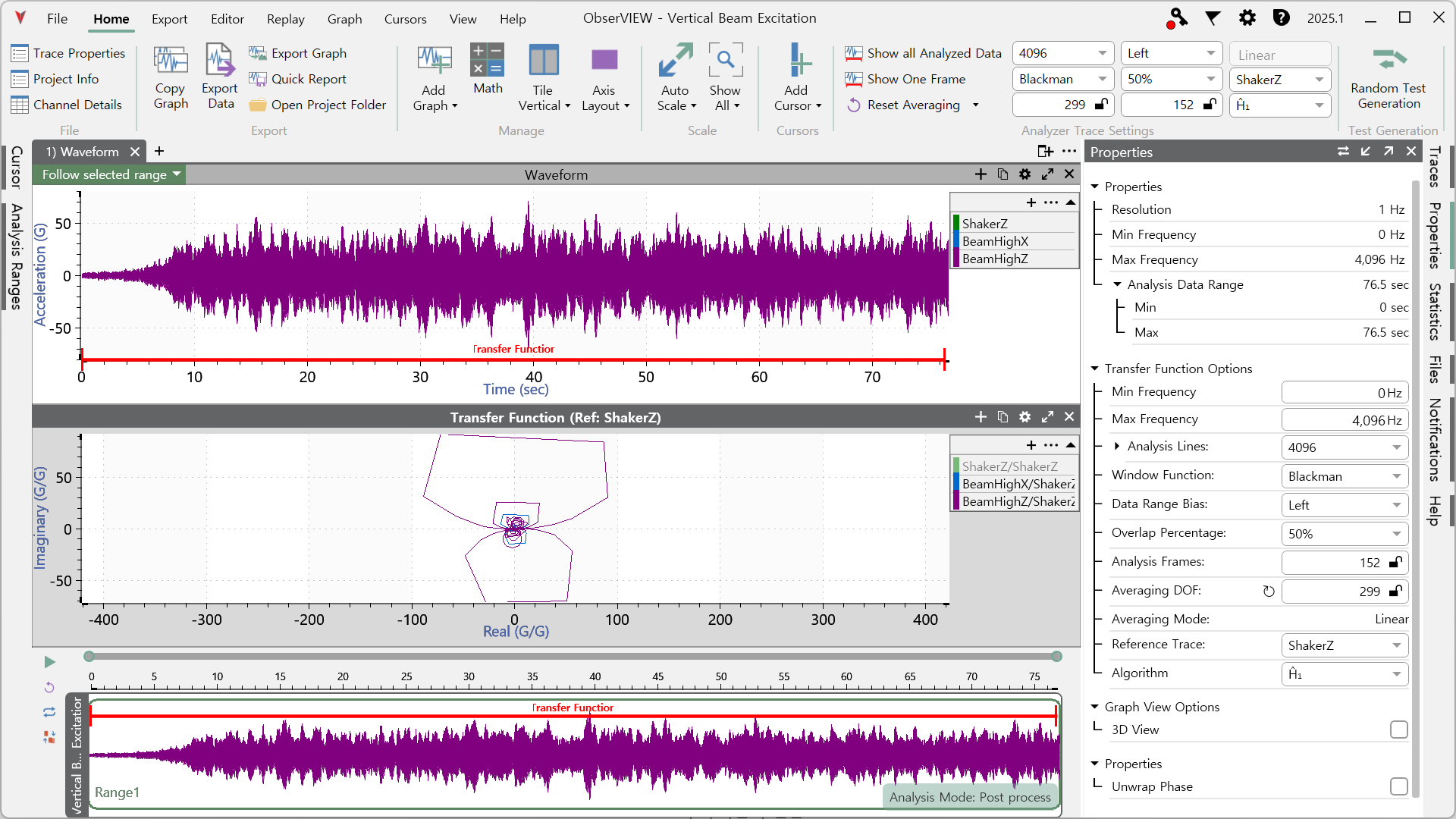
Nyquist 플롯은 Complex 플롯과 유사하게 복소 평면에 응답을 그리지만, 특히 제어 시스템의 안정성 분석이나 모달 안정성 평가에 특화된 분석 방법으로 쓰입니다. x축은 실수부(real), y축은 허수부(imaginary) 또는 그 부호를 취한 값으로 하며, 주파수가 변화함에 따라 응답이 복소 평면에서 그리는 궤적(루프)을 나타냅니다. 

이 방식이 유리한 경우는 다음과 같습니다:

• 개방 루프(open-loop) 시스템의 안정성(피드백 루프의 폐루프(closed-loop) 안정성)을 평가하고자 할 때. 
• 복잡한 구조나 시스템에서 모드의 안정성, 결합, 감쇠 특성을 모달 분석(modal analysis)과 함께 보고 싶을 때. 특히 진동 제어나 피드백 기반 시스템에서 유용합니다. 
• Bode 플롯이나 단순 복소 플롯만으로는 파악하기 어려운 복잡한 상호작용, 또는 비정형 응답 / 불안정 가능성을 종합적으로 분석하고자 할 때

즉, 제어 시스템 설계, 피드백 기반 진동 제어, 혹은 모달 해석과 안정성 평가를 함께 진행할 때 Nyquist 플롯이 적합합니다.

 

1) 큰 루프 = 저차 모드(1차, 2차 같은 굽힘 모드)

복소 평면에서 큰 루프는 구조물이 강하게 반응하는 공진(모달) 주파수를 의미합니다. 루프가 클수록 해당 모드의 진폭(모달 참여도) 이 크고, 시스템이 그 모드에서 크게 에너지를 흡수하거나 방출함을 나타냅니다.

플롯의 형태를 보면, 세 채널이 거의 같은 궤적을 그리므로 3개 측정 지점이 모두 같은 모드 형상의 영향을 강하게 받고 있다는 것을 보여줍니다.

 

2) 루프 크기 → 모달 강도

큰 루프는 해당 모드에서 출력 응답이 매우 크다는 뜻입니다. 즉, 이 빔은 특정 저주파 영역의 굽힘 모드에서 큰 변형을 보이고 있습니다.

 

3) 루프의 넓이 → 감쇠(damping)

루프 폭이 좁을수록 감쇠가 작고, 넓을수록 감쇠가 큽니다. 그래프를 보면 루프가 비교적 넓은 편은 아니라,
감쇠가 매우 작은 금속 빔의 전형적인 모달 특성을 보여줍니다.

 

 

해당 내용과 관련해서 팜테크에서 시스템 솔루션을 제공하고 있습니다.  관심 있으시면 아래 홈페이지 또는 연락처를 통해 문의 주시면 됩니다. :)

 

https://famtech.co.kr/sub04/01_01.php

팜테크